Dear friends and specially those so brave to still read what I write, hallo!
In the last months I have received partly very emotional and in times personally aggressive replies to my report on this subject! Such reaction s are expression of underlying reasons that induce people to respond! On one side, and fully understandable, the subject of this subproject of my building from scratch the sailboat model I named Carina, is pretty distant from what naval modelist usually present!
On the other side I have gotten such reactions from 2 different communities. One are the naval modelists, and this in all languages I deal with, spanish, english and german, so it is pretty much across cultural borders, the other source is from forum members dealing with physics!
The naval modelist and real sailboat skippers argue along the lines that implementing a pulley with seven sheaves as it was used on the original sailboat Endeavour does not work on a model with a scale of 1:20! The basic argument here is, after accepting the fact that my systems concepts has no problems to deal with changing the length of the sheet by up to 8400 mm, that the friction in the sheaves makes the sailboat inoperable due to the friction between the rope and the sheaves in the pulley!
The community dealing with physics argues about totally opposing lines of arguments. They say there is only the friction between the sheave and the axis and that by using ball bearing as I plan to do this friction is neglectable!
So you can see that depending from the background the experts are coming you get to completely different results about the issue of the friction! I want, nevertheless add, that a real sailboat skipper that has a small pulley on his sailboat wrote that effectively the friction represents a major factor when operating his real sailboat. What he wrote is that the friction between the rope and the lateral walls of the blocks has a major effect!
So advancing my studies on "System Physics", the way I want to apply the impact of physical effects in my model and the preliminary results from my investigations on the subject of friction in the sheaves of a pulley. I have felt able to give a call to the physics institute of the highly respected Munich university, Ludwig Maximilian Universität, short LMU. There I was lucky enough to get hold by phone of a scientist willing to respond to my questions.
I presented to him the fact that I was planing to study Physics for the Bachelor degree, but that as a person with serious health problems I had to teach the subjects upfront myself, something as will never ever get a job in the industry, gave me the time to do so! I presented to him the two view points I have met and just presented to you, I told him about the limitations of the Euler-Eytelwein-Formula that just represents a formula, not with an "=" sign, but with an unequal symbol =<, that basically says that the real friction impact could be up to the value computed when replacing the unequal sign by an equal sign. I also told him that I had found out so far that even for the classical mechanics in Physics you met very different ways to deal with the same aspects of physics in mechanics giving as an example the classical physics way as reflected i.e. in the Euler-Eytelwein-Formula, but also the views and methods applied by System Physics and by topological manifolds! It became apparent by his reaction that he was willing to take my question seriously and he laughed when I talk about those different ways to deal with mechanics.
His explanation about the reactions from the physics community towards the friction in the pulley was due to the fact that many physics view the physical issue from an idealized perspective and that in this view it was correct to say that only the friction of the bearing of the sheaves was present. But that in real world due to diverse reasons even without the rope slipping around a sheave there was a friction component that could be relevant and that the inequality symbol used in the Euler-Eytelwein-Formula was due to those aspects that impacted the exact amount.
I informed him further That I had started to study a Master-Thesis hat dealt with the friction between cylindrical bodies and a rope and that did analyze the friction is sailor nodes using the mathematical method of finite elements. For your information dear readers without the intention to lecture those of you that do well know the issue, the finite element mathematical method is a method that computes problems by splitting an object into infinitesimal fractions and integrating the results to get the grand total. So it is what is called a numerical or discrete mathematical method that approximates its results depending onto in to how many sections it splits an object.
Simply stating it, it uses the mathematical power of computers to compute a subject split into many, many pieces and adds them to get the final result.
Well, this is one of the reasons why i decided to use tools that combine modeling and simulation with strong mathematical capabilities and due to many reasons I believe I have already tried to explain I decided to use the software from Wolfram Software, Mathematica and SystemModeler. So I can start modeling my sheaves and the pulley with seven of those using the modeling and simulation capabilities of Modelica, an essential element of SystemModeler and to use Mathematica to compute, i.e. by the finite element method as applied to the friction between a rope and a cylindrical body, here the sheaves in my pulley, as described in the Master-Thesis I downloaded a copy from.
But any modeling and consecutive simulation results depends in a very essential way from the quality of the models used! And exactly here comes into play what i have presented earlier in this thread, the "Hardware-in-the-Loop", short HiL, and "Software-in-the-Loop", short SiL, for which the Teensy 3.1 and the RaspBerry Pi B+ boards have been purchased. I will have to define experiments were I can compare the data resulting from measuring in the experiments and the data generated through simulations using those models! mathematica offers so called "solvers" that can generate equations that follow the experimental data at the minimum error defined and so adapting the models to the real world data.
May be, if I do not die earlier due to my health problems this thread and other similar ones in the different forums that I use to get support and feedbacks, I will be able to present the facts resulting from modeling the pulley. I am completely aware and I do accept the following possible results:
1. The experts from the physics forums are right and friction using ball bearing in the sheaves is irrelevant for the operation of my sheet control system in my model scaled 1:20 to the original Endeavour!
2. The experts from the naval communities are right and the pulley is not able to produce results that do not render my sailboat model inoperable due to the friction in the pulley!
3. Any results between those two contradicting positions, or may be even a completely different and unexpected result.
But what will definitely be a result if I succeed to accomplish the modeling and simulation of the pulley in my sheet control system, is that i will know and understand the relevant and irrelevant parameters and their impacts! With the following graphic, simple and full of errors, but still the best i have, I will try to present what really understanding the friction in the pulley and the impact of the design parameters have.
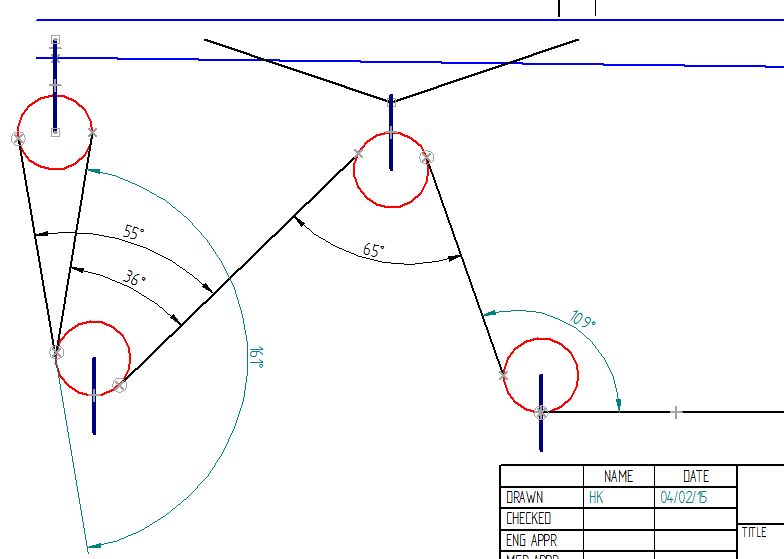
If you look on this drawing and if you keep in mind that the angle with which the rope embraces a sheave has a major impact on the friction to the movement of the rope around each of the individual 7 sheaves of the pulley, you will see that where you place those blocks containing the sheaves has an important impact on the angle with which the rope embraces a sheave! If the distance horizontally between the sheaves increases, the angle will get smaller. by smartly selecting the diameters of the sheaves this can additionally be influenced.
Now you have to be aware of, that the "Momentum" used in System Physics to represent mechanical systems and the pulley is such a mechanical system, requires to analyze and consider independently the momentum in the 3 directions of space, Px, Py and Pz, it becomes apparent that the proper choice of the cartesian coordinate system is relevant.
The X-axis of a cartesian coordinate system would be along the center line of the hull, the Y-axis would be parallel to the water surface, horizontal and perpendicular to the center line of the hull and the Z-axis would be vertical. As usual the problems arise when you start to deal with details! Would the position (0, 0, 0) of this cartesian coordinate system be at the floating line level of the hull, means placed at the height of the water surface, would it be better placed at the rotational axis height around which the hull rotates when due to wind pressure in the sail i.e. gets inclined, or would it be better placed at the height of the boom? This is just reflection about where to place the origin of the cartesian coordinate system along the vertical axis!
The orientation of the Y-axis is probably less difficult to decide? It should be parallel to the water surface! But where along the X-axis and the Z-axis? Along the Z-axis i have already presented the issues above. Should it be placed where the hull rotates when turning around it, or should it be placed where the rotation axis of the boom of the sail is?
But with the Z-axis it is a bit more complicated. The questions as to where it has to be placed along the X-axis raises the same question as to where is the rotation axis when the hull turns left or right? Should the orientation of the mast be the direction, so that any rotation of the boom keeps the Z-axis value of the boom along the length of the boom the same, and so on!
The issue to be considered from the mathematical complexities resulting from a bad choice of the reference coordinate system. if an axis of the coordinate system at the same time is the axis around which rotational movements take place, computation is simple, if not, then it is more complex. But besides the complexity of the computations of equal importance is to keep it adequate so that the interpretation of simulation results is kept as simple as possible!
So to summarize the issues around the selection of the proper cartesian coordinate system, ignoring that there are also other coordinate systems. Any object could move in 6 ways, called the number of degrees of freedom of the movements!
An object can move along any and all of the 3 coordinate axis , the first 3 degrees of freedom of movement, each resulting in its own formula to describe the movement of an object along those axis, a total of 3 of what are called translational movements and as a result translational mechanics.
But the same object can also rotate around each of this 3 axis, those are 3 additional degrees of freedom of movement an object has and as a result you can have 3 more formulas or equations that describe the objects rotational movement and as a result we talk about rotational mechanics.
The method I plan to use is to have a reference cartesian coordinate system which has its origin at that location in 3D space where the 3 axis around which the sailboat hull can rotate. Additionally I will use auxiliary coordinate systems that are placed in such a way that the mathematical description is kept as simple as possible. So as a result there will be equations that describe how to convert coordinate values from an auxiliary coordinate system to any of the auxiliary ones used This conversion equations between different cartesian coordinate systems are relatively simple, but the key is that the computations taken place in the adequate auxiliary coordinate systems will keep the mathematics as simple as possible and make it much easier to understand the results within those auxiliary coordinate systems. lets take an example of one auxiliary coordinate system assuming the "reference cartesian coordinate system" to be as explained at the beginning of this paragraph!
In one such auxiliary coordinate system the X-axis would follow the direction of the boom and the Z-axis the mast! So in the plane defined by those 2 axis is where the sail is located, what ever position the sail and its boom might have in relationship to the hull. So if the sailboat leans to one side by 30°, this would have no effect on the auxiliary cartesian coordinate system. The same applies to the X-axis when the boom rotates. Lets assume the boom rotates to the center line of the hull by 45°. The Y-axis of the auxiliary cartesian coordinate system, being oriented vertically to the plane defined by the X-axis and the Z-axis of the auxiliary coordinate system would follow the rotation of the other 2 axis.
So to convert a coordinate value described by the auxiliary cartesian coordinate system to the reference value we would combine by applying the 6 degrees of freedom equations that describe the movements of the auxiliary cartesian coordinate system and so get the values in the reference coordinate siýstem!
So what i just described and has to be applied to the 3 momentum equations for translational mechanical movement and to the 3 rotational momentum equations. Now you can see that just by describing the 6 degrees of freedom of an object and having as a result 6 equations is what the Modelica simulation environment has to do with the equations included in a model! So the modelica environment takes advantage of this "knowledge" to generate automatically and invisible to the user i.e. what I just presented to do the computations required to simulate a system using the models that describe this system!
Here is where the object oriented implementation of the language Modelica comes into play! When I define a proprietary model of a system or any part of it I start from using object classes given in the "standard object library" of Modelica. So mechanical objects in this library, be they translational or be they rotational have in their classes already included the properties that such mechanical translational or rotational objects have and those are inherited in the new classes that I define using objects from the standard library!
So key for any beginner and apprentice like I am is to grasp this concepts and learn to properly apply them when designing our own objects and to use this knowledge when interpreting the results of simulations! Finally I have been told that this weekend i will receive a copy of the brand new version of the Modelica master book, so that I can learn and study it! Let me reemphasize this! I am new into this, I am a beginner and I am an apprentice. So making the assumption I am lecturing you is far away from being so! All I am doing is to share with you, the same way we do it when writing a report from scratch, the up and downs when dealing with the challenges I encounter and as an optimist I am, to may be find some valuable advice from you my dear few readers left! But let me also emphasize it! Even those that get emotional and sometimes offensive as a reaction to my reports. The fact that I have been confronted with such behaviour and attacks from the naval modelist community and from the physics community has been of incredible value to me! The fact that those 2 communities have opposing and conflicting opinions about the friction in a pulley as I am planing to implement in my sailboat model at a 1:20 scale, is in its own right a valuable piece of data for me!
Believe me. Just getting to the point were I felt capable to contact a physics scientist at the physics institute at the LMU and ask the question has taken a large effort from my side! To ask the question properly i did face 3 challenges, at least!
1. Understand and put in context the statements received from experts in the naval modeling community.
2. Understand and put in context the statements received from experts in the community pf the physics.
3. To be able to formulate my question such that my counter part at the LMU took my question seriously!
4. To be able to put the former 3 sources in relationship to refine the objectives of my design by modeling.
I am certain and not yet even close to be able to grasp the problems I will encounter when dealing with the mathematics in this context! And so I am not even able to say what questions I might have that I will present in the mathematical communities in the proper forums. I know, that the very little I have been improving my studies just to get back and up to speed with the mathematics I once knew when I joint the university and I was an excellent student at school kind of just enabled me to have a framework of understanding of what those mathematical courses that form part of the bachelor of mathematics and of physics are all about. They really are not more than just the basics skills required to get away from beeing a mathematical analphabet. As a result I have an idea about the mathematical methods available and I have the means to know where to look in to acquire the knowledge in the different fields of mathematics as the need pops up! I hope that learning to use the software tool Mathematica will help me to overcome my lack of experience in applying mathematics by understanding enough of the mathematical methods and of the use of the software Mathematica to "use" the mathematics for my goals. I am very explicit! I am in doubt if I ever will have the courage to say about myself to be a mathematician, but I do have the hope to be enabled to apply mathematics as required for reaching my objectives!
As we are in a naval modeling website i would like to add 2 pictures from the self made sheaves that I plan to use in the blocks that will make up the pulley in my sailboat:


This sheaves i did make using my lathe in aluminium and I have inserted a ball bearing and allow for an axis with 2.5 mm diameter and have an external diameter of 20 mm and an internal diameter for the rope of 12 mm. The height of 4 mm of the shoulders I hope will allow me to prevent the 0.9 mm diameter Aramid rope to get in touch with the wooden case of the block in which the sheave will be installed!
 Author
Topic: Design by Modeling (Read 8562 times)
Author
Topic: Design by Modeling (Read 8562 times)



